Elena A. Ivanova St. Petersburg State Polytechnical University

Substantiation of the model of body-point of a general kind

Let us consider the body-point, the inertia properties of which are characterized by the mass m and two spherical tensors of inertia. The moments of inertia determining the spherical tensors of inertia are equal to mB and mJ. The kinetic energy K, momentum K₁, proper angular momentum K₂ and the angular momentum calculated with respect to a reference point Q have the form:

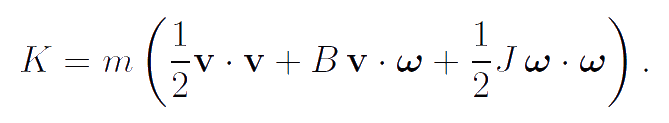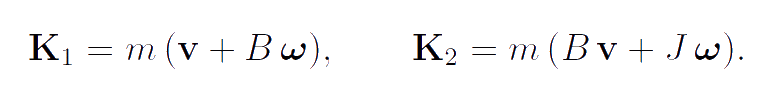This body-point represents the body-point of a general kind which is not an infinitesimal rigid body. The additional inertial parameter B gives this body-point the dynamic properties which are not inherent to rigid bodies. The motion of a body-point is described by the equations of Euler's dynamics:

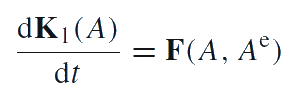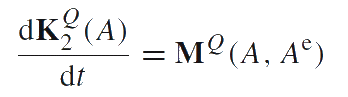Here F(A, A^e) is the external force, M^Q(A, A^e) is the external moment calculated with respect to a reference point Q. The equations of Euler's dynamics, written in the form presented above, are hold for any closed body A (the body which which does not exchange mass with its surroundings).

In order to clarify the meaning of the parameter B we discuss the solution of the following model problem. We consider the material system (see Figure) consisting of the frame and N rigid bodies attached to the frame by means of elastic springs. For simplicity we suppose that all bodies can move only in the line of axis x and и rotate only on axis x. We introduce following notations: m, J are the mass and moment of inertia of the frame; the corresponding quantities with index i are the mass and the moment of inertia of rigid body number i. The kinematic characteristics of the system are the displacement of frame along axis x, the angle φ of rotation of frame about axis x, and also the displacement x_i and angle of rotation φ_i of rigid body number i relative to the frame. The springs are considered to be elastic helical lines whose property consists in the fact that when twisting in one direction they become longer and when twisting in the opposite direction they shorten. Conformably, when stretching and pressing the springs become twisted in different directions. We suppose that the internal energy U_i of spring number i as well as the force F_i and the twisting moment M_i modeling the influence of spring number i on the frame take the form:

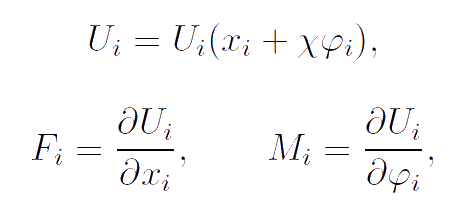Let us assume that we can only observe the motion of the frame and cannot see what is happening inside the frame. Assume that the spring connecting the frame and the internal bodies have a sufficiently high stiffness in order to the period of free oscillations of the internal bodies would be much shorter than the characteristic time associated with the motion of the frame. We also assume that with instruments we can measure only the average values of the quantities characterizing the motion of the frame. The purpose of further research is to suggest an approximate model of the system, which takes into account the integrated effect of internal structure on the motion of frame. We start with the formulation of equations of motion of the frame and internal bodies:

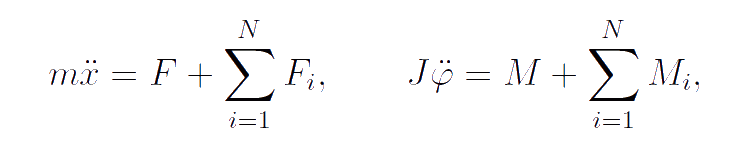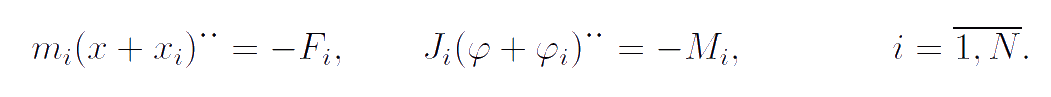Here F and M are the external force and the external twisting moment acting on the frame. Analysis of equations of motion shows that the translational and rotational motions of the frame are interdependent. If there is no external moment acting on the frame and the initial angular velocity is equal to zero, then because of the internal dynamics of the system the frame become to rotate. If there is no external force acting on the frame and the initial velocity is equal to zero, then because of the internal dynamics of the system the frame become to move.

Example. Let us consider the motion of the system represented in Figure under the action of the external force and twisting moment being linear time functions. For simplicity we assume that all internal bodies have the same mass and moments of inertia, the internal energies of the springs are the quadratic forms of deformations and all springs have stiffness equal C. In this case we have:

Let the oscillation period be much smaller than an observing time on the motion process. In that case the characteristics of the motion averaged over a period can be interested. After some formal transformations and time averaging over the period of free oscillations of internal bodies we eliminate the variables describing motion of internal bodies and obtain the following equations for the quantities that characterize the motion of frame:

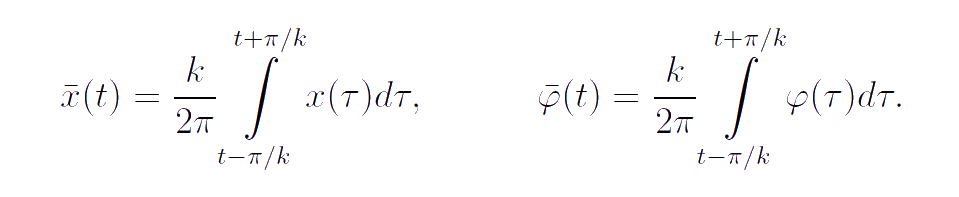The parameters in the above equations are expressed in a complex manner through the parameters of the original model. In line with the formulation of fundamental laws of mechanics the left-hand sides of the equations of motion are the time derivatives of momentum and proper angular momentum. Indeed, if the reference point Q is on the axis x then the first term in the expression for the angular momentum vanishes and the derivative of proper angular momentum remains on the left-hand side of the second law of Euler's dynamics. It is clear that the expressions for momentum and proper angular momentum appearing in the averaged equations of motion are the same as the above expressions for these dynamic structures of the body-point of a general type which is not infinitesimal rigid body.

Conclusion. Thus, the influence of the internal structure of the system on the motion of the frame can be taken into account both by means of the internal forces and moments and by means of the additional inertial parameters ensuring the interplay of translational and rotational motions. A more detailed description of this model can be found in the paper:

• Ivanova E. A. On one model of generalised continuum and its thermodynamical interpretation. Mechanics of generalized Continua (Ed. H. Altenbach, G.A. Maugin, V. Erofeev). Berlin: Springer, 2011. P. 151-174. (400 Kb)

To view PDF files you can download free version of Adobe Acrobat Reader.

Guidelines to view the publications